A Kind of a New Music Box
      
             Rudy’s PolyParadigm Sound Visualization Box PPSVB x.11
             
          

Dr. phil Rudolf Kaehr
copyright © ThinkArt Lab Glasgow
ISSN 2041-4358
( work in progress, vs. 0.4, Dec. 2015, August. 2014 )

A Tool Box for sonic and visual deep-structural adventures
by comparing classical, indicational and morphic CA

Motto

If words are not going to be listened to and notions are not  going to be understood, there is still a chance of showing some pictures and making some noise, with an offer to motivate to enjoy or to conceive their differences and also to try to overcome the attitude of blind and deaf denial of conceptual thinking.

Classical CA

Jaime Rangel-Mondragón, A Catalog of Cellular Automata
“A one-dimensional CA processes in parallel the simultaneous change of state of each individual cell forming a collection arranged in a line. These individual changes are performed in accordance to the states of each one of their neighbors including itself through the application of a local transition rule. It is remarkable the fact that from such a simple mechanism we are able to generate a behavior of profoundly intricate complexity, all this in contrast to the general impression that effects are always preceded by causes of at least comparable complexity.”

http://library.wolfram.com/infocenter/MathSource/505/CAcatalog.nb

More at:
http://plato.stanford.edu/entries/cellular-automata/supplement.html

Hence, three categories of paradigmatically different kinds of CA are studied. The first is well known and gives a contrastive background to the two newly introduced kinds of CA.

Firstly, the classical CA,
secondly, the indicational CA,
thirdly, the morphogrammatic CA.

Therefore I introduce a new kind of an epistemological comparatistics, i.e. a comparison of graphic and sound systems in respect to their paradigmatical structures based on different kinds of writing systems and their own intrinsic CA rule sets.

In a first approach, aspects of the dynamics of CA systems in general are studied by the presentation of their intrinsic transition graphs.

Transition graphs for classical CA had been introduced and exhaustively studied by Andrew Wuensche. The used implementation in this paper utilizes the published version of Stephen Wolfram.

“Cellular Automaton State Transition Diagrams” from the Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/CellularAutomatonStateTransitionDiagrams/

Furthermore, the proposed approach to a formalization of morphogrammatic CA is still more a simulation than a genuine implementation of the very concept of morphogrammatic CA.

The classical paradigm is well studied, mathematically and philosophically, and got a decisive elaboration with the Opus Magnum of Stephen Wolfram’s A New Kind of Science (NKS).

Here, I refer just to some 1D CA examples within the set of CA rules. Accessible by special CA of the CA box.

A special topic of compararison is the representation of the single archetypical figures of Sierpiński triangles in the 3 modi of formalization (classical, indicational and morphic).

Interactive results are realized with the formats CDF and HTML.

RuleBox of the ReLabel-based rules

MorphogrammaticRuleDefinitions

Relabeling

StaticMorphoRuleDefinitions

DynamicMorphoRuleDefinitions

DynamicMorphoRuleSchemes

Diagram of the separation procedure

http : // memristors.memristics.com/CA - Compositions/Memristive %20 Cellular %20 Automata %20 Compositions.pdf

Motivation and definition of the rules

Epistemological orientation

On the level of a functional implementation of the morphic cellular automata, like in this paper, the genuine concept of morphic interaction is replaced by a corresponding set of 'pre - given' functions in look-up table of functions.

The look-up concept relates to memory, while the operational appraoch is producing its ‘operands’ by the application of the operation.

Look-up is depending on a selected alphabet and the functions over it.

The operational approach is not depending on a pre-given set of rules, organized as a look-up table, but is operationally creating its operands over any symbolic input.

What is presumed is a set of rules (operators), symbolized as morphograms, and not as a set of functions.

Hence the system of morphograms is presented as a system of operations.

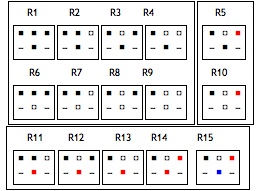
Paradigmatic system of CA rules

The Stirling turn indicates a reversion/subversion of the known logical order of semiosis. In this conceptual graph, semiotics turns from the fundamental center - position to a derived mode of writing with trito - grammatics playing the role of the initial position of the graphematical writing system.

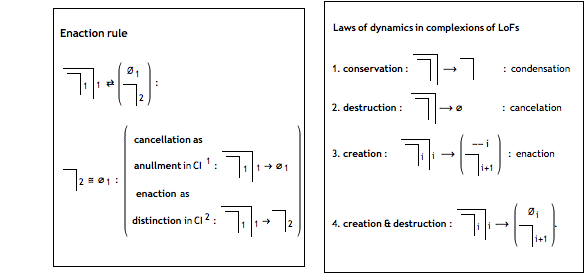
Laws of Form

The indicational way of writing and thinking, introduced by George Spencer Brown (GSB) with his Laws of Form (LoF), published 1969, is not specially well elaborated and got a very controverse reception from the side of mathematicians and logicians.

One of the most crucial intuition of the CI is the “topology invariance” of its terms of distinctions. Therefore, the indicational CA introduced here are based on this “topology invariance” of the distinctions only and are not yet including the internal CI rules of the Laws of Form (condensation, cancelation).

A distinction of a distinction is conceived in the reflectional CI, i.e. CIR, and CIRT, as both at once: as annullment and as reflection (enaction). Therefore, annulation is eliminating and destroying distinctions while reflection as enaction is not only creating new distinctions but also a new domain, i.e. world of distinctions, in which the new distinction and its further applications is realized.

Morphogramatics

The morphogrammatical way of writing and thinking, introduced by Gotthard Gunther with his “Cybernetic Ontology and Transjunctional Operations,(1962), is as such well elaborated by the publication “Morphogramatik”, Kaehr, Mahler (1993), and got a some controvert reception from the side of mathematicians, logicians, semioticians and cyberneticians.

Morphograms had been introduced by Gunther as pre-logical patterns (morphé) of trans-classical logics. As pre-logical and pre-semiotic figurations morphograms are in fact figures and rules at once, i.e. as figurations or structurations. The dynamic aspect of morphograms as rules is implemented in the paradigm of morphoCA.

In his theory of cybernetic self-reflection, Gunther classified the 15 basic morphograms into 3 classes:
1. Acceptance: objective reflection represented by the morphograms ,
2. Rejectance:  subjective reflection represented by the morphograms
3. Refutation: self-reflection as reflection on 1) and 2) by .

In the context of cybernetic studies of dynamic systems, this classification had also been interpreted in the 1960s by Henz von Foerster as order principles.

Cybernetic Dynamics
1. Order from order,
2. Order from disorder,
3. Order from noise (order and/or disorder).

A new graphematic principle of order and creativity might be added as:
4. Order from (neither order nor disorder).

Because this cybernetic research into automata theory happened in the early 1960s, it wasn't mainly computer supported.

Definitions

How GSB sounds might be listened at the register CI, is orchestrated by ruleCI.
The further CI concepts, CIR, RCI and CIRT, had been freely introduced by the author in previous papers.

The rule set CI, defines the objectional definition of the Calculus of Indication (CI), a reflection on CI generates a second-order CI, i.e. the RCI, with its genuine new rules.
Further reflectional thematizations of the CI generates a third-order calculus RCI, and its augmentation CIRT.

Indicational CAs are thus divided into:
a) first-order indCA (in the sense of the Calculus of Indication (CI), ruled by the set of ruleCI,
b) as second-order (enactional) rules ruleCIR,
c) as third-order rules ruleRCI, and
d) the rules of ruleCIRT.

Rule schemes for indicational CA

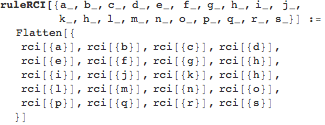
Rule schemes for morphic CA

Morphogrammatic CAs are divided into:
a) classical morpho , ruled by ruleCl, with complexity 4,
b) trans-contextural CAs, , ruled by static ruleM, with complexity 5,
c) trans-contextural CAs, , ruled by dynamic ruleDM, with complexity 5,
d) trans-contextural CAs, , ruled by ruleMN, with complexity 6 and
e) trans-contextural CAs, , over-dtermined, ruled by ruleMNP, with complexity 7,
f) trans-contextural CAs, , over-determined, ruled by ruleM42, with complexity 8.

Cl rule set    = [1,2,3,4,6,7,8,9} over 4 places,
M rule set     = { CL ∪ {5,10,11,12,13,14,15} over 5 places,
MN rule set   = { M} over 6 places,
MNP rule set = {M} over 7 places.

MorphoCA rule schemes

Motivations

After Niklas Luhmann got mesmerized by the performances of the magician Heinz von Foerster (Second Order Cybernetics), the Laws of Form nevertheles nurtured a whole movement over decades of mainly German theoretical sociologists.

Finally, the morphogrammatic endeavor is more or less unknown to the academic public. It goes back to Gotthard Gunther’s work in the 1960s at the Biological Computer Lab, Urbana, Ill. on a reflectional theory of living systems capable of self-reflection and autnomous decision making.

It is certainly not my aim to enter into a 'debate' about 'deviant' or 'cranky' (Hao Wang) formal languages.

There is also no need to go back to the Ancient Chinese thinkers, Pythagoras or Kepler to connect conceptions with numbers and sound.

It suffice to reduce the apparatus to an elementary construct that has shown to be quite powerful.

Cellular automata have a long history but might have come to the public awareness only by computer-supported experiences.

The challenge of this exercise is to hear and see concepts, i.e. structurations, and not just to perceive sounds and pictures.

This seems to be possible mainly by a comparison of the (deep)structure of different sound and graphic systems based on specific cellular automata.

Epistemologically different perceptive systems are not properly defined by their internal differences but by the difference between their deep-structural differentiations.

A nice, and well developed structuration is established with the difference of classical, indicational and morphogrammatic writing systems as proposed in my texts towards a general theory of writing systems, called graphematics.

Also sounds of different graphematical systems are heard and pictures are seen, there is nevertheless a crucial difference in their mode of production.

The slogan, What you see is what you get, applies properly for classical approaches of a visualization of concepts and a way to present sound.

The indicational approach is still in the framework of the classical semiotic conceptualizations and modes of writing. Because the fundamental ‘topological invariance’ of its mode of writing which is not directly percievable it demands for some combinatorial manipulations of the notation to be possible to perceive in a classical mode of perception its genuine abstraction properly.

The morphogrammatic approach is denying the obvious WYSIWIYG concept. Therefore, What you see and hear is not what it is. Morphogrammatics is a part of kenogrammatics. The term ‘keno’ in kenogrammatics derived from the Greek kenoma (κένωμα, emptiness) says it all: there is nothing to tell.

The WYSHINWIS, “What You See and Hear Is Not What It iS”, challenges towards a new kind of perception: the cognitive perception, that is at once, a perceptive cognition.

The set of paradigms, the classical, the indicational and the morphogrammatic, is certainly not exclusive. There are other kinds of conceptualizations and writing systems to recognize too. This is explicitly developed in the research field of graphematics, the morphosphere(s).

Hence, the aim of this little exercise presented here, is to learn and to train the brain to recognize the difference between different conceptual systems as they are presented to our perception by sounds and graphics and not their intrinsic beauty or lack of it.

Neither are there any mathematical or philosophical considerations included in this proposal of an exercise.

One exercise might be concentrated mainly on the single form of Sierpiński triangles, and its variations in graphic and sonic environments. It then could be seen as a kind of a contemplation on Wolfram’s ECA rule 90. In this case such exercises are restricted to strictly symmetric patterns of homogeneous or heterogeneous dynamics.

Technically I apply freely David Burraston’s “Music Box Toy with Elementary Cellular Automata”.

What do we have to do to follow this invitation?

Compare, contemplate and analyze your experiences!

The rules of the presented CA are new and had been introduced by the author as an experimentation to deal with morphogrammatic and indicational CA.

This work of different paradigms of formal systems goes back to publications that did not yet use Mathematica as a programming environent.

David Burraston's program "Music Box Toy with Elementary Cellular Automata".

“This Demonstration uses a simple and novel mapping of elementary cellular automata (CA) to single - voice musical sequences. The mapping is created by evolving a small CA through all its possible initial conditions for a number of generations, converting the cells to decimals and storing them in a table. This table is visualized using Mathematica' s built - in function ArrayPlot with starting conditions assigned vertically and generations evolving horizontally.” (David Burraston)

More at: http://noyzelab.blogspot.com.au

David Burraston, Music Box Toy with Elementary Cellular Automata
http : // demonstrations.wolfram.com/MusicBoxToyWithElementaryCellularAutomata/Wolfram Demonstrations Project
Published : January 31, 2012

How to use the programs?

How to compare sound and visual events?

Again, my intention is not to simulate any known kinds of anthropologically founded music and sounds but to let the algorithms, as far as possible, ‘manifest’  themselves thru the machine. The same holds for the visualizations. There is no intention to imitate any mental patterns, cognitie, archetypical or halluzinatory.

Hence, my not so humble intention seems to be to enable a project that evokes “a kind of a new kind of music of no kind”.

It might be a late contribution to Bruce Stirling’s remark at the Academy of Media Arts, Cologne around 2000, that he preferred very much more to see/hear the machine manifesting itself instead of imitating, simulating and varying human achievements in music and poetry.

A different intention is expressed by:

Stephen Wolfram: “How difficult is it to generate human-like music? To pass the analog of the Turing test for music?”

http://blog.stephenwolfram.com/2011/06/music-mathematica-and-the-computational-universe/

Katarina Miljkovic’s mixed approach

“Generative sound is always coupled with live performance of some kind, often improvisation, to contrast and enrich the mechanical aspects of electronic part.”

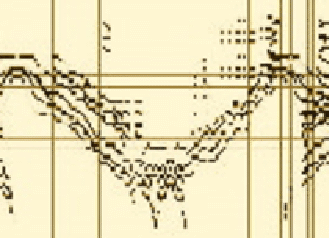
More CA sounds: Music simulations versus algorithmic sounds

Morphic​Algorithms, Rudolf Kaehr, Glasgow 2014

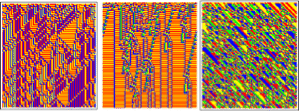
Orientation thru different paradigms and categories

The sound and visualization programs are both based on the same morphogrammatic production rules for 1D cellular automata.

Therefore, the comparison of both types of events is strictly one-to-one.
That is, the category ruleM of the sound box corresponds directly to the category ruleM of the visualization box.
And this holds also for all other categories.

The graphematic rules are classified in 3 categories:
1) morphogrammatic:
a) static rules: ruleCl, ruleMN, ruleMNP, ruleM42 and
b) dynamic rules: ruleDM,
both rule sets have a simple or a random seed (init),
2) the indicational rules: ruleCIR, ruleCIRT, and
3) the classical CA rules: CA rules.

Additionally, there are some selected rules too: special M and special CA.

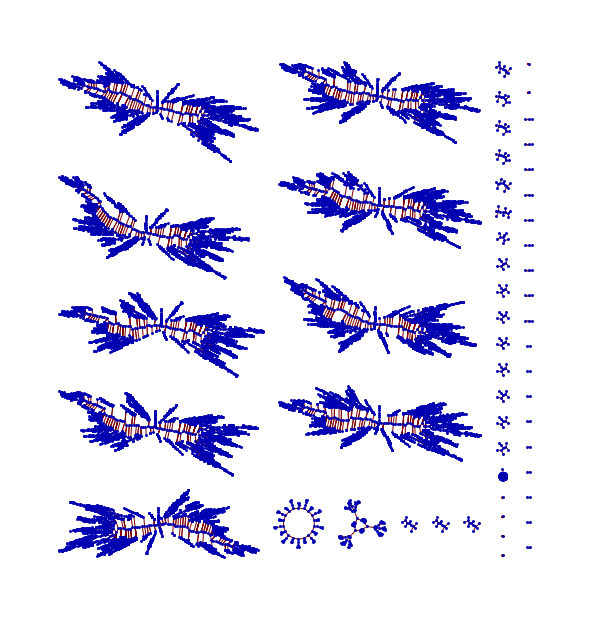
The offered direct graphic representations of the sound production, as shown by the sound box, is more complex than the underlying strict production rules for the cellular automata. Its complexity is defined by the complexity of “all its possible initial conditions for a number of generations” (Burraston).

Therefore, a separate visualization of the direct production rules with a simple or a random initial condition, seed, is offered too.

Comparisons

Comparison is part of the general project of Comparatistics that is comparing on a paradigmatical level different kinds of writing systems (symbolizations).

The topic “comparison” gets algorithmic support by several programs published by Daniel de Souza Carvalho at Wolfram Demonstrations Project.

A nice, slightly modified example for formal comparisons is given with Carvalho’s “Elementary Cellular Automaton Dynamics as Wavelets”.

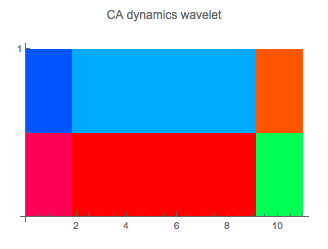
How to use the sound box?

A full description of the categories can be found in Burraston’s paper.

• cells:

• generations:

• mapping:

• transpose:

• duration:

• instruments:

• show mesh:

How to use the graphics box?

• n (steps) glider for the number of ‘generations’

• steps offers a set of fixed steps.

How to use the transition graph box?

• width: complexity of the environment

• states: set of the morphic states in symbolic form

• icons: set of the morpho rules in symbolic form

Initialization Code for PPSB-ruleSets

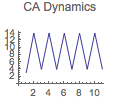
Dynamic Sonic Events with PPSB.x11

ruleDM 13, 5

Morphogram: ruleDM

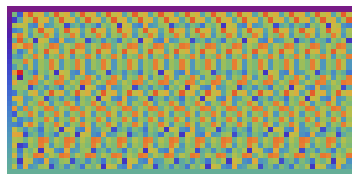
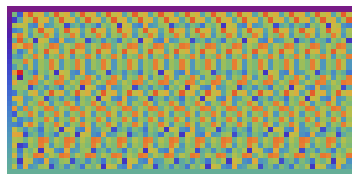
Dynamic Visualizations of PPSB.x11 events

Morphogram: ruleDM

Visualizations: morphic and indicational rules

ruleDM 60, 44

ruleM, static + ruleDM, dynamic, RandomInteger[1,111]

ruleDM 65, 111, Random

ListAnimate ruleDM, Random, 222

Descrete Colors

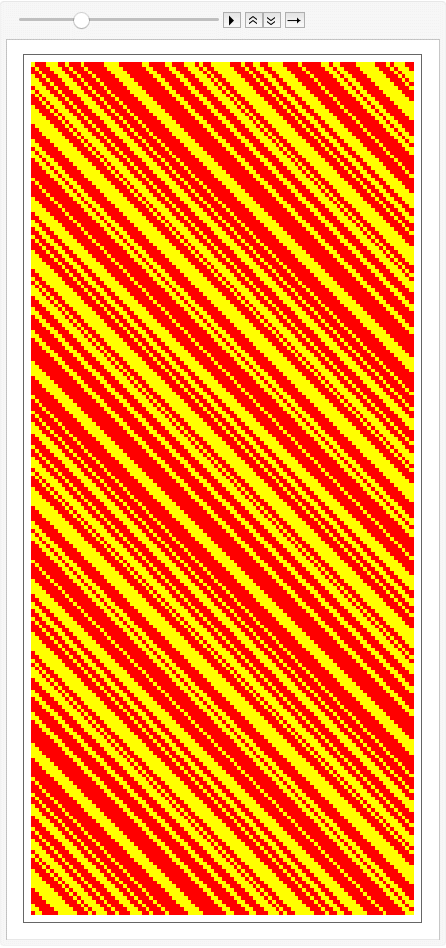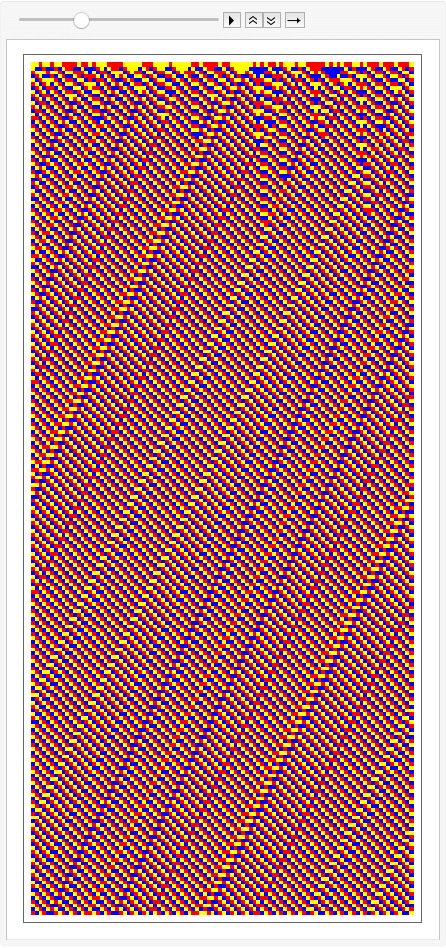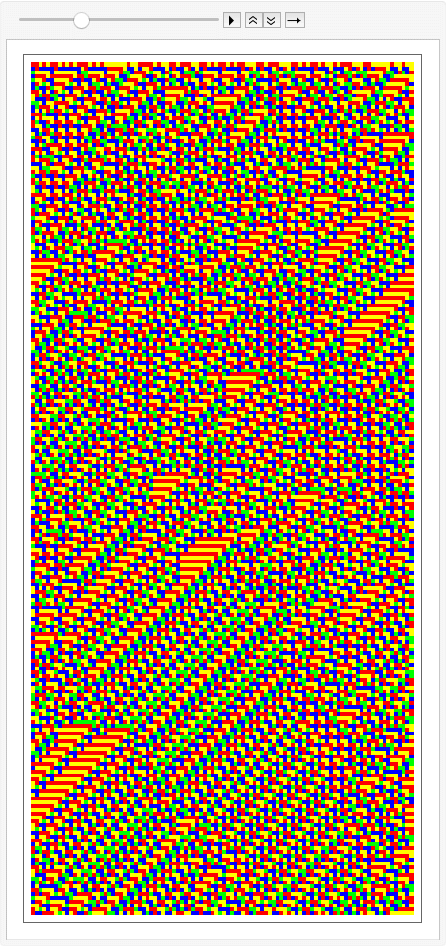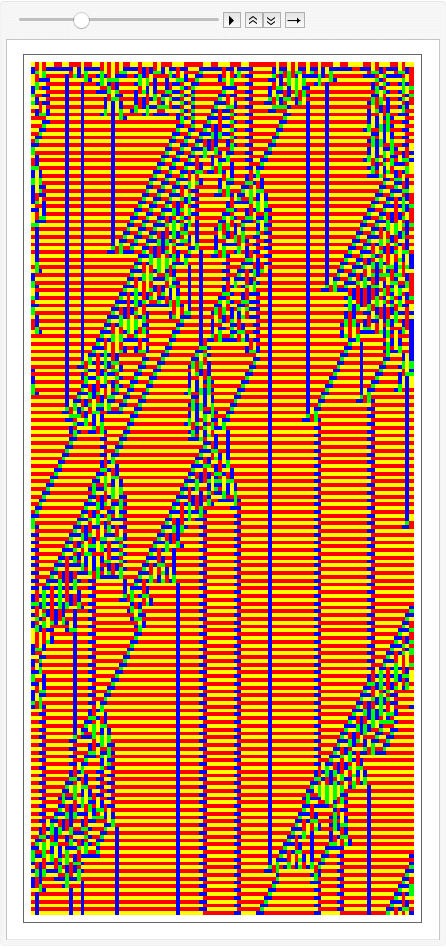
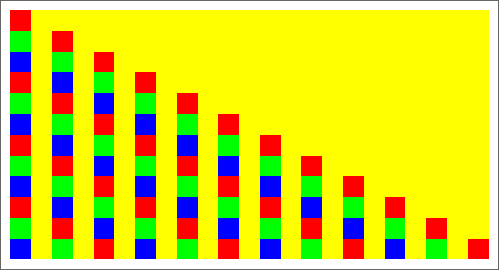
Rainbow Colors

Morphogram: ruleDCKV

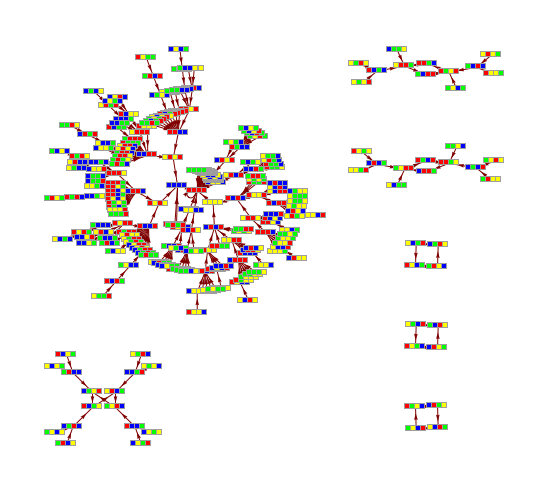
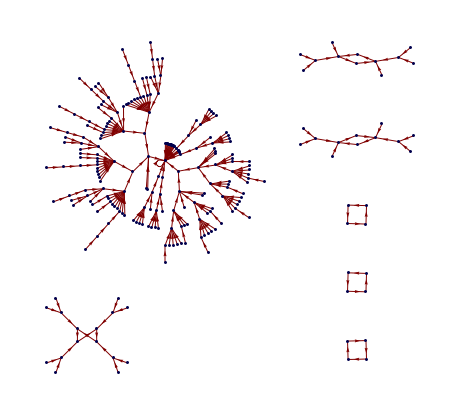
Transition Graph representation of PPSB.x11 events

Transition graphs for morphic and indicational CAs

Transition graphs for classical CA

Stephen Wolfram, “Cellular Automaton State Transition Diagrams” from the Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/CellularAutomatonStateTransitionDiagrams/

Transition graph of CA rule 110, width 3

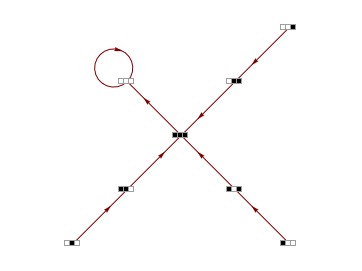
Transition graph for ruleCIR

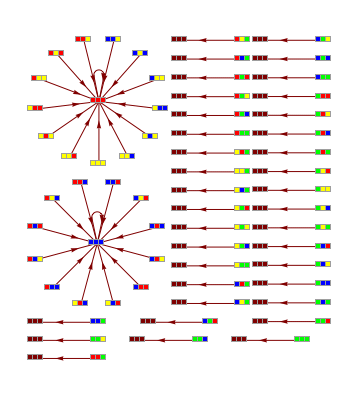
Transition graph for ruleDCKV

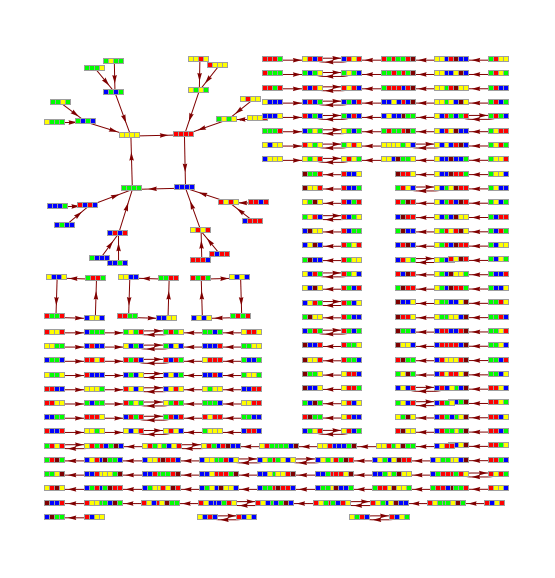
Comparatistics of picto-, diagrammatic and sonic manifestations of the ruleMN18

CA vizualitation of rule MN18, {9, 44, 47, 4, 0.1, 103}, witdth 4

Transition graph for rule MN18, {9, 44, 47, 4, 0.1, 103}, witdth 4

Sonic rule MN18, {9, 44, 47, 4, 0.1, 103}, 2252.8 s

Different  number of cells

6 cells

5 cells

Examples of vizualisations of the morphic ruleDM, RandomInteger[1,100]

Complete plot table of vizualisations of the morphic rules ruleDM

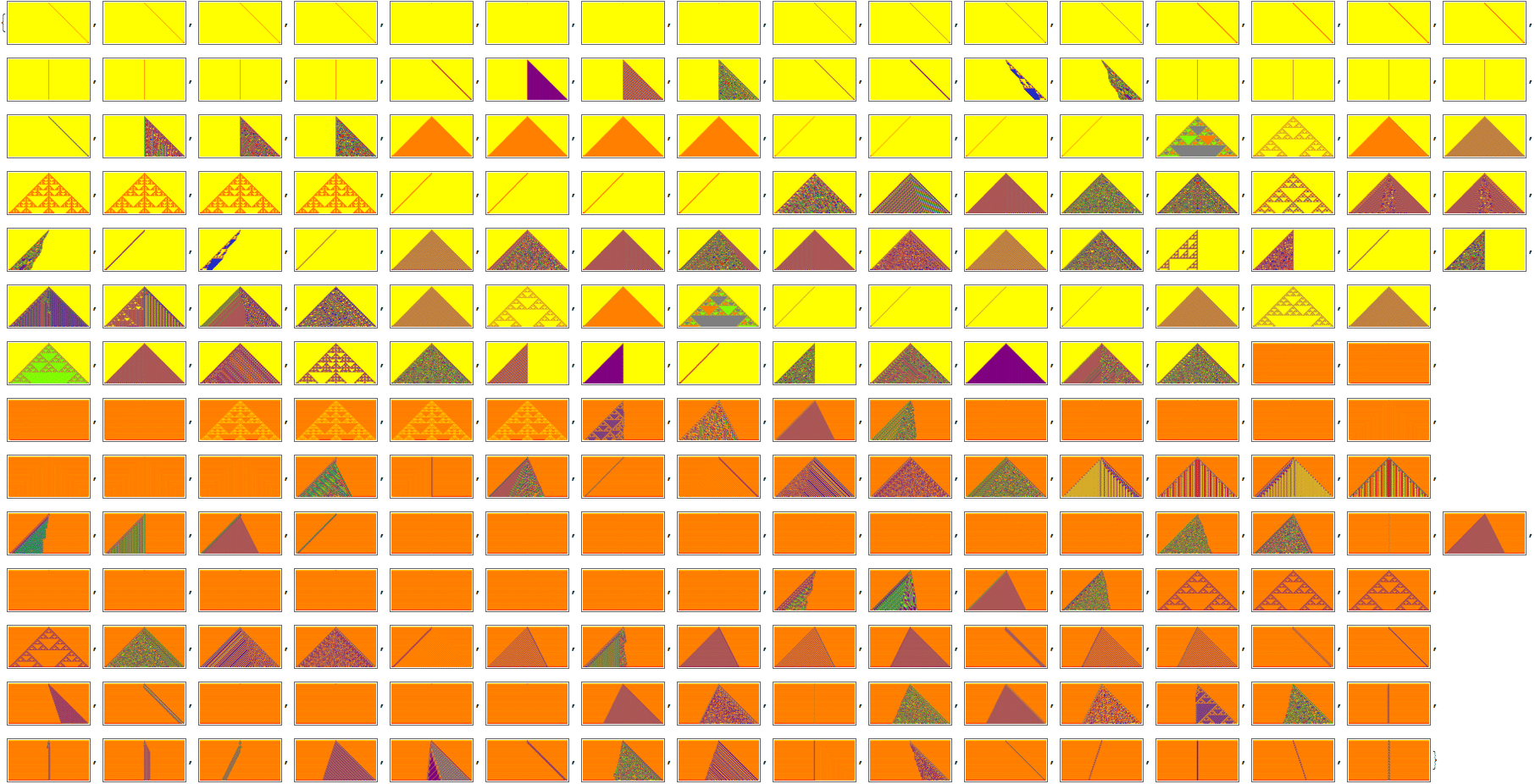
Complete plot table of vizualisations of the morphic rules ruleDM, RandomInteger[1,100]

Special cases of ruleDM Random

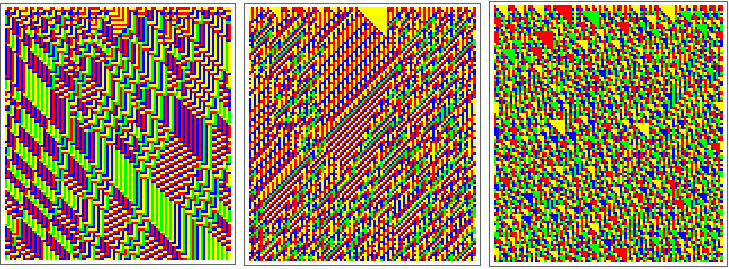
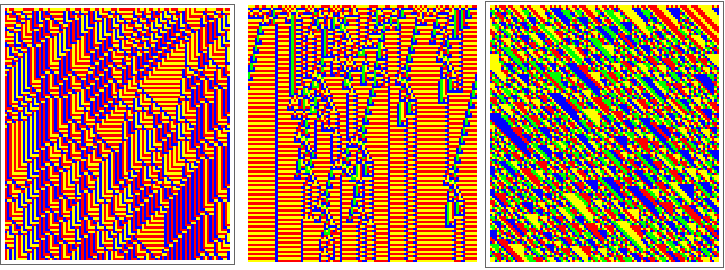
Transition graphs

Transition graph for ruleDM[{1,2,3,4,10}] -> “DM2”

Colored transition graphs

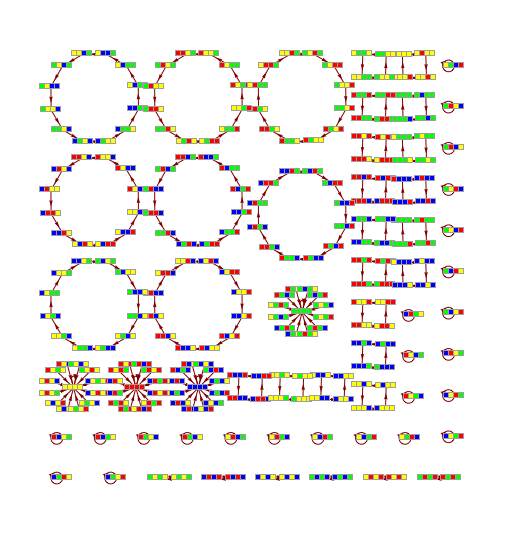
Naked transition graphs

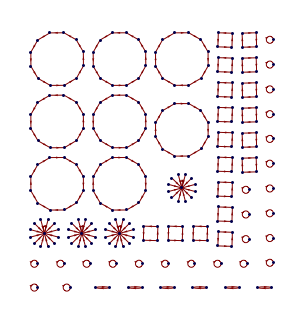
Transition graph for ruleDM 24 and ruleM 24, width = 4

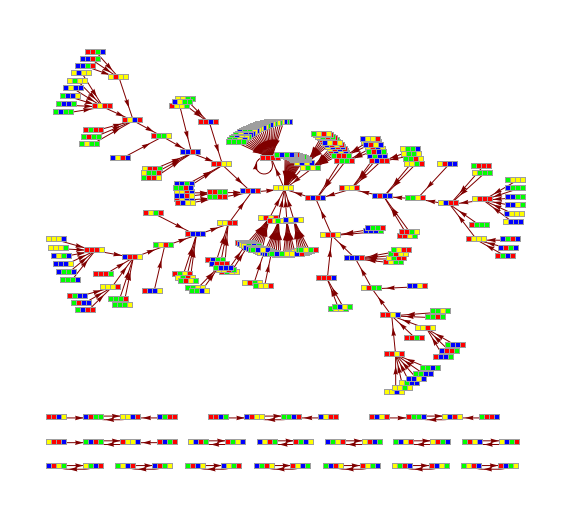
ruleM 24, ruleDM 24, width = 3

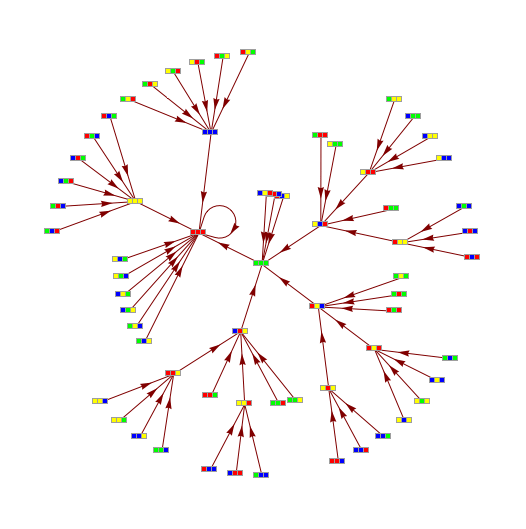
Table for ECA:
http : // atlas.wolfram.com/01/01/views/40/TableView.html

Transition table for ruleDM, w=4

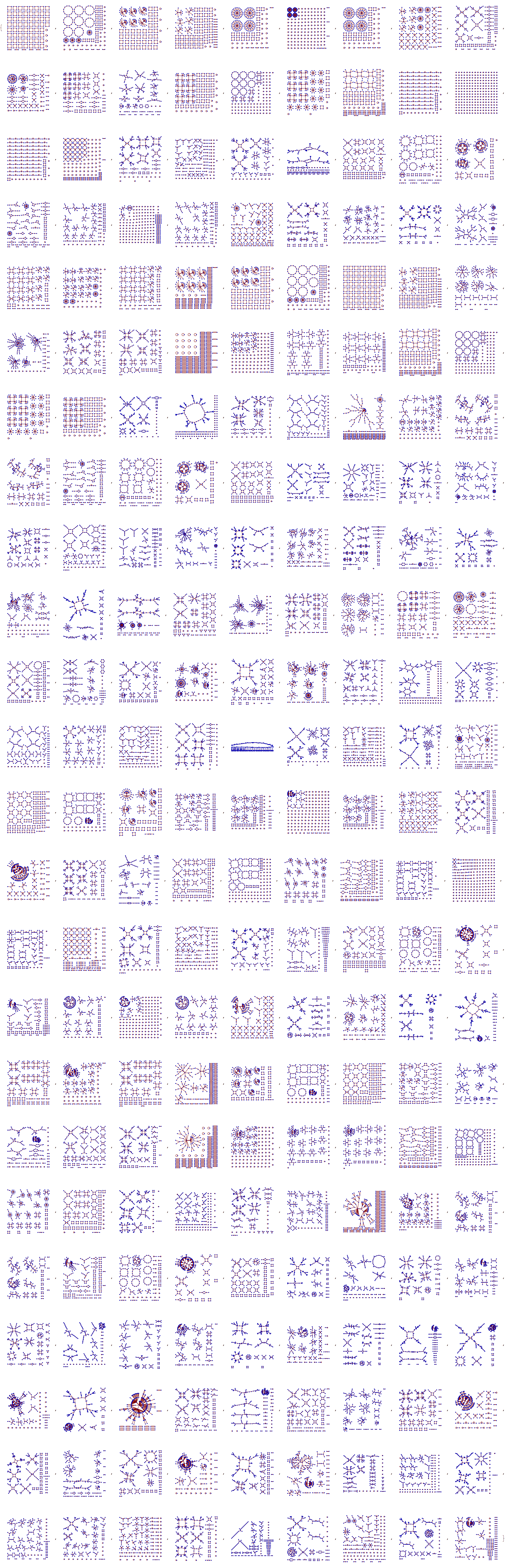
Transition table for ruleDM, w=5

Butterflyoids?

Transition graph for ruleMNP[{1, 7, 12, 13, 10, 14, 15}], Tuples[{0,1,2},9]