TIME, TIMELESS LOGIC

For more than two millennia, all Western scientific thought has rested on the methodological principle of two-valuedness dividing all reality into an objective and a subjective component. The division was assumed to be exhaustive. The existence of a third value of basic ontological significance was expressly denied. The ensuing system of logic not only posed the questions but also circumscribed the range of permissible answers. One of the two available values was considered to be designative, and the other had to be nondesignative in order to obtain a set of laws interpretable in ontological terms. The designative value was called positive; it pointed to the purely objective aspect of the universe. And since the nondesignative or negative value could not point at anything, the trend of all Western science, based on this system of logic, has been one of progressive objectivation to the exclusion of all traces of "subjectivity "-which are implied in the nondesignative value.

From the very outset, the participants in the disc ussion disagreed. The Eleatic school of thought excluded Time from objective existence. But Heraclitus considered the static aspect of the universe as deceptive. Accord-ing to him, no thing is identical with itself; its ultimate essence is an event. A seeming advantage of the Eleatic viewpoint became visible as soon as Archimedes appeared on the stage of scientific inquiry. With him begins a trend that G.J. Whitrow [²1] has called the "elimination" of Time from natu-ral philosophy. This trend has continued up to the present, where it mani-fests itself as the absorption of Time into Einstein's geometry of a hyper-space. Between Archimedes and Einstein, innumerable arguments have been advanced in favor of its elimination; and during the history of Western sci-ence, their persuasive power has grown stronger and stronger. But each argu-ment which spoke for the elimination of Time has been countered by an equally strong one advocating the retention of Time as a basic constituent of objective reality. Especially in recent times, the pro and con arguments have grown more and more sophisticated. And if we continue along this line of inquiry, we may expect them to become even more subtle and penetrating.

However, recent developments in logic make us wonder about the genuine-ness of the, whole controversy. If no final answer has been found for 2000 years, we are entitled to the suspicion that there may be no answer. And this suspicion is supported by two data which the controversy of natural phi-losophy has not yet taken into account. First, the scientific development leading from Archimedes to Einstein was accompanied by a parallel trend- the history of dialectic logic. And dialectic logic poses an entirely different question. Its first concern is not the relation of Time to Being, but the relation of Time to Logic itself. It can be shown that the discussion of Time on the basis of natural science remained incomplete and insufficient because it ignored the dialectic aspect.[³2] The other datum which throws a significant light on the alternative of elimination or nonelimination of Time is the comparatively recent insight into the consequences of the isomorphic character of two-valued logic. This isomorphism is based on the principle of the Tertium-non-datur (TND), the duality of conjunction and disjunction, and the fact that in classic logic the dividing line between designation and nondesignation coincides with the distinction between assertion and nega-tion. This isomorphism has a peculiar result. It divides. all potential objects of logical discourse into two basic categories-for the first category, the isomorphism is irrelevant; for the second category, it influences the logical treatment of the object of discourse. We shall call the objects of the first category "ortho-objects" and those of the second "pseudo-objects." An ortho-object is something that can be conceived apart from anything else. An apple we eat is an example of the first category. To know what an apple is, we do not have to refer to plums or grapes. The second category contains such objects of thought as cannot be conceived without reference to some- thing else. Terms referring to this category are: left and right, positive and negative, life and death, rest and motion, and also the temporal terms past and future. In these cases the meaning of one term implies the meaning of the other.. With regard to the pseudo-objects the isomorphism of classic logic has the following effect: Each statement we may make about them is refutable by a contradictory statement; for each pseudo-property we ascribe to a pseudo-object, we shall find a contradictive pseudo-property we can ascribe to it with equal right. And since Time is such a pseudo-object, we might expect the controversy to continue forever as to whether or not it is eliminable.

We shall take the following stand: It is useless to continue the controversy because the question is badly posed and can never lead to a final answer. But if the problem of Time does not permit a definite answer as long as our two-valued logic is applied to it, we have no choice but to question the competency of classic logic in this special case. Aristotle himself seems to have taken this attitude when he confronted his logic with the phenomenon of Time. The part of the Organon called "Peri Hermeneias" raises, in its notori-ously obscure Chapter Nine, the question of the validity of the total disjunction between contradictive statements, if such statements refer to future events.[⁴3] Aristotle's analysis of the problem yields two results: First, the TND is unconditionally valid for past as well as for future events. But it is applicable only to the Past and Present. It is not applicable if we form statements about events which will only occur in the Future. The second result of the chapter is more or less implied. Since the issue is one of applicability, the distinction between what-there-is as Past or Present and what-there-will-be as Future requires the existence of a self-referential system. Aristotle does not say so himself, but the inference was drawn in the later development of classic logic from Boethius to William Ockham.[⁵4]

Aristotle's distinction between the validity of the TND and its applicability is unfortunately rather vague and permits two different interpretations. The first and more obvious one suggests that statements about future events have only probability or modality values filling the logical distance between false and true. This interpretation of the text was utilized for a premature attempt to develop a theory of many-valued logic. However, it has been shown that systems of probability or modality do not display a rigidly formal structure and, if reduced to their purely formal constituents, revert to classic logic with full applicability of the TND.[⁶5] It is significant that all endeavors to develop a many-valued logic on this philosophic basis have led to theories that could logically account for only a very small fraction of the enormous wealth of constants that turn up in many-valued logic.[⁷6] These attempts, started in 1920, have now practically been abandoned.[⁸7] However, the hints Aristotle gives about the relation between Logic and Time permit a different interpretation. Since Aristotle significantly groups Past and Present together with regard to their logical relevancy, we may say that the TND is valid, first, with reference to past events and, second, with reference to the dichotomy between Past and Future. TABLE 1 may illustrate what we mean. It displays the pattern of the classic table of negation but in an iterated form. The large table represents the total disjunction between Past and Future. Inside the larger table we find the same pattern as a subtable, but now as an alternative between positiveness and negativeness. Both tables represent symmetrical exchange relations and testify to the unrestricted validity of the TND between the respective members of the exchange relation. It follows that, if the connection between the two tables is ignored, Time displays a basic symmetry. If both tables are made to cooperate, we obtain a logical system in which Time will display features of symmetry as well as non-symmetry.

TABLE 1 may be interpreted as a three-valued system which is composed of three two-valued subsystems. Since the Past is a context of what did actually happen and what could have happened but did not, the relation of the Future to the Past is ambiguous. First, we have a two-valued relation between the Future and the Past as what came to pass; but we have also an exchange relation between the Future and the Past as that which did not come to pass. If we add these exchange relations between values to the classic ontological exchange relation between what is and what is not, we obtain our three two-valued systems. However, TABLE 1 shows us even more. We may say that it demonstrates the application of the TND between a single value - in our case (3) - and a two-valued system represented by the values (1) and (2). We need not add that placing the subsystem (1 ¨Æ 2) under the heading of the Past is a mere convention. One might as well interpret the Future as the potentiality of an open alternative of what might and what might not come to pass; and the Past as the one-valued singularity of what-there-is and what-there-has-been. Such interpretations serve only illustrative purposes. Nothing is relevant but the relational structure formed by these three two-valued systems. However, for the foundation of a logic which intends to encompass the phenomenon of Time, a more basic concept has to be introduced. Classic logic is traditionally considered as the doctrine of the laws of thought. These laws are supposed to regulate the activity of a computing system or subject which maps its environment. They refer, by designation, to an outside world and, by self-reference, to themselves. In other words, the classic two-valued system represents two ontological loci which we may conventionally call Thought and Being. On the other hand, it is obvious that Time will not fit into either of them. Its two-valuedness of Past and Future is neither identical with the contraposition of affirmation and negation inside our consciousness; nor is it identical with the alternative between self-referential consciousness and objective world. This seems evident. But if the two-valuedness of Time has its ontological locus neither inside the consciousness nor in the environment of a self- referential system, we must ascribe to it an ontological locus of its own. In the case of a two-valued system, the difference between value and locus is so small that it hardly yields more than the mere distinction between logic and ontology. But the introduction of a third locus widens the gap between them sufficiently -so that a special symbolic representation for the loci is required.

We, therefore, introduce a new type of symbol which we shall call a "kenogram." Its name is derived from the term "kenoma" in Gnostic philosophy, which means ultimate metaphysical emptiness.[⁹8] An individual kenogram is the symbol for a vacant place or ontological locus that, in conjunction with other kenograms, may form a pattern without regard to possible value-occupancy. An individual kenogram may or may not be occupied by one value at a time. To provide for the accommodation of many different values at the same time, we may introduce as many differently shaped kenograms as we choose. As symbols for values, we use positive integers. We further stipulate that a context of individual kenograms shall be written as a vertical or horizontal sequence. This affords us two possibilities. We may either repeat a kenogram of the same shape until the predetermined length of the sequence is filled; or we might choose differently shaped kenograms to fill our vertical columns. A kenogram may remain empty within the context of a calculus, or it may be occupied by a value.

For value-occupancy the following rules shall hold: kenograms having the same shape must always be occupied by the same value; the choice of the value, however, is free. Kenograms of different shape must carry different values, if any. Several kenogrammatic sequences of equal length added horizontally to each other shall form a kenogrammatic structure, provided all sequences are present which follow from its generating rule. Repetition of a sequence would constitute redundancy. The horizontal width of ascending orders of structures will be determined by how many differentiations we are ready to introduce. If we exhaust all possibilities, four basic distinctions will be available. We shall call them, in ascending order of differentiation:

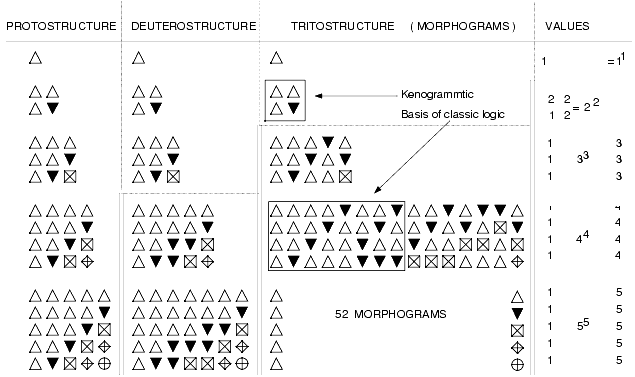
The first three comprise the kenogrammatic range of a transclassic logic. TABLE 2 begins with a vertical minimum sequence of one place. Thus, there can be no structural differentiation either in the kenogrammatic field, nor between kenogrammatic structure as a whole and structure by value-occupancy. If we proceed to two-place sequences, there is still no differentiation between protostructure, deuterostructure and morphogrammatic structure. But there is a difference between kenogrammatic structure in general and value-occupancy. We notice that the two vertical kenogrammatic sequences permit four value- occupancies. If we proceed to three-place sequences, we observe that the number of columns for trito- or morphogrammatic structure has increased. Morphogrammatic structure now differs from the two preceding kenogrammatic orders. There is, however, still no distinction between protostructure and deuterostructure. If we finally step down to four-place sequences, the table shows the protostructure and deuterostructure may also be distinguished.

Protostructure represents the absolute minimum of kenogrammatic differentiation. In this case, we ask only how many vertical lines are required if the placing of an individual kenogram is irrelevant and if we want only the absolute minimum of kenograms to be iterated. Our placing the shapes within a sequence is entirely arbitrary; any other distribution would do as well. If we proceed to the deuterostructure, we still consider the place into which an individual kenogram is put as irrelevant. But, whereas in the protostructure only the upright triangle was iterated, we now ask: If otherwise the conditions of the preceding protostructure held, what is the highest number of iteratable kenogrammatic shapes? We find that in four-place sequences (where protostructure and deuterostructure begin to differ), only two kenograms permit iteration. For demonstration purposes we have chosen the two triangles. The place where the iterations appear are still arbitrary choices.

We have offered this short description of TABLE 2 in order to show why, in the history of Western science, there has been a marked tendency toward the elimination of Time. The logical formalism on which the spirituality of the West is based permits only a two-valued system of logic, assuming two ontological loci represented by two kenogrammatic symbols. Thus, it was impossible to assign to Time an ontological locus of its own. One of the two available loci had to carry Time in addition to whatever else it was carrying. This imposition of Time on one of two ontological loci already occupied by Being or Thought produced an intolerable epistemological situation; and scientists since Archimedes followed a very sound instinct when they tried to eliminate Time as a basic ontological category. Two kenograms do not produce sufficient structural differentiation to give Time an equal partnership with Being and Thought. For the primordial distinction between object and subject, the stark dichotomy between empty structure and value-occupancy was sufficient; but to conceive Time as apart from Being as well as from Thought, a differentiation within kenogrammatic structure is necessary. This requires the introduction of a third ontological locus and its symbolic representation in the kenogrammatic pattern.

Zeno's paradox stemmed from the fact that Being stands for the class of all ortho-objects designated by a single value. Time, on the other hand, belongs to the first class of pseudo-objects which require designation by a duality of values. When Zeno confronted Being and Time, he effected, formally speaking, a confrontation between value-singularity and value-duality.[¹¹10] It is obvious that no two-valued system can display all the features which Zeno's problem implies. The introduction of a third value is the first step to bring Time within the range of logical analysis.

TABLE 3 presents the pattern of designation for m-valued systems. The first vertical column on the left gives the total numbers of values for a given system. The double line, descending in ever increasing steps, separates designation from nondesignation. The numbers which appear on both sides of the double line do not represent individual values but give the sum of values required for a specified designative or nondesignative purpose. Where a zero appears, no value is available. The table starts with the one-valued system; and since a nondesignative value is not available, such a system cannot properly be called a logic. It represents an ontology that provides a "theme" for a subsequent logic. The next step leads us to the two-valued system which is indeed a logic, since one-valued designation is here reflected in a nondesignative value. These two systems make up the total formal structure of our traditional thinking; and as long as we are content with the simple contraposition of ontology and logic, we have no motive to go further. This elementary distinction corresponds to our formal differentiation between value-structure and kenogrammatic structure in general, with no kenogrammatic subdistinctions. However, if we refused to pack Time into the ontological loci of Being and Thought, we learned that we had to proceed to at least a three-valued system. This step formally establishes the ontological difference between ortho-objects and pseudo-objects. Since we have found that the identification of Time as an ortho-object involves us in paradoxes, we may assume it to be a representative of the first class of pseudo-objects. On the other hand, a pseudo-object requires, as we noted, at least two values for designation- otherwise, there is no structural characteristic to set it apart from the ortho-objects. This leaves us no value for nondesignation. In other words, a three-valued system is again no logic at all, but the formalization of a first transclassic ontology.

M	DESIG.	NON-DESIGNATIVE
1	1	0	ONTOLOGY (MONO- THEMATIC) \| LOGIC
2	1	1
3	1	2	0	ONTOLOGY (POLY-THEMATIC )
4	1	2	1	\| LOGIC \|
5	1	2	2
6	1	2	3	0	ONTOLOGY (POLY-THEMATIC )
7	1	2	3	1	\| \| LOGIC \|
8	1	2	3	2
9	1	2	3	3
10	1	2	3	4	0
11	1	2	3	4	1
12	1	2	3	4	2
...	...	...	...	...	...

Such an ontology implies two modes of designation: designation by a single value and also designation by a duality of values. Classic logic has only one ontological theme-Being as objective permanence. Thus, it is monothematic. All transclassic ontologies are poly-thematic. The classic ontology, represented by a single designative value, is retained in all transclassic ontologies; but to it, at least a second theme, represented by a duality of values, is added. Only in the second theme does the problem of Time become fully accessible to formal logical procedure. In order to develop logical systems to correspond to the first poly-thematic ontology, we have to introduce nondesignative values. This can only be done if we progress to a four and five-valued system. An ontology with two themes requires two successive systems of logic because its conceptualization has to choose between one or the other theme. Either the first or the second theme will shift into logical focus or, to put it in more formal terms, nondesignation will either correspond to the, theme designated by the single value or it will reflect the second theme which needs a duality of values for designation. TABLE 3 shows these cases as four- and five-valued systems. The ontologically emphasized theme is indicated by underlining the appropriate numbers on the left side of the double line. What is not underlined is only carried along as a subtheme. The two designational systems that follow the first poly-thematic ontology demand, of course, the introduction of a fourth and fifth ontological locus.

This prompts the question: What do these new ontological loci signify? The shortest possible answer is: Being, its reflection in Thought, and Time represent the whole range of objective existence as reflected in three-valued ontology. Yet there must be a subject of cognizance conscious of an objective world. This subject must be capable of distinguishing between the world as outlined in its ontology, its thought-image of this world, and itself as being the producer of the image. Since the first three loci refer to the world, the fourth locus must accommodate the image making and the fifth the producer of it.

At this point our departure from classic logic shows its most striking aspect. Our three-valued ontology encompasses Thought (as image) as a component of the environmental world. But as a process Thought occurs again in locus four. This reoccurrence is due to the inherent ambiguity of the term "Thought." It may either refer to the image, or the the image-producing process. The classic tradition of formal logic neglects this ambiguity. And thus it does not understand the Janus-face of subjective self-reference. Subjectivity is both the still image of the world as well as the live process of making an image; and what we call a personal ego constitutes itself in the triadic relation between environment, image and image-making.

However, the act of self-reference which establishes the ego represents a detachment of the subject from the environment as well as from its own thoughts. The fifth ontological locus provides the place for it. The subjectivity which is aware of Being, Thought and Time is distributed over the loci which follow our three-valued ontology. The first four loci give us the full range of kenogrammatic distinctions. But something is still missing: the structural feature which indicates the detachment. Detachment by selfreference means, logically speaking, iteration or repetition. And this is just what the fifth ontological locus supplies. Five-place sequences add nothing to the distinctions between protostructure, deuterostructure and tritostructure; they only repeat them. Even the fact that only two kenograms are iteratable reoccurs.